Exam Development Process

Standardized tests are used at all levels of education, in multiple assessment contexts, and for a variety of purposes. They can help teachers, educators, employers, and policymakers make decisions about students, other teachers, jobseekers, employees, or even programs and institutions. It is essential that standardized tests provide unbiased and accurate data, metrics, and information, and hence meet the highest professional, technical, and industry standards.

OpenEDG Python Institute certification exams are designed to measure proficiency in specific areas of knowledge, skills, abilities, and aptitude for performing specific tasks. At the same time, they should provide a fair, valid, reliable, credible, and secure source of information.

OpenEDG Python Institute's exam and certification development process is rigorous, comprehensive, and collaborative. We adopt a meticulous, consultation-driven, and competency-oriented approach to test design, test development, and test implementation, utilizing qualitative development frameworks, subject-centered design patterns, and psychometric modelling mechanisms.

The exam development process consists of a number of inter-related stages:

Market Research and Analysis – the foundation of the entire development process. Exams and certifications are designed and developed following a rigorous process of industry and market research involving Job Task Analyses (JTAs), Training Needs Analyses (TNAs), Skills Gap Analyses (SGAs), and a number of qualitative and quantitative studies carried out to identify the job descriptions and the actual skills toolkit sought by employers, and the skills taught at schools, in order to bridge the gap between the education and industry sectors, and make sure that certification holders are equipped with all the necessary means they need to pursue and advance careers in IT and programming.

Syllabus Development – this stage involves recruiting SMEs (subject matter experts) for the purposes of defining exam objectives, defining the target audience (job task analysis and evaluation of professional standards), preparing exam documentation, and carrying out the initial process of pre-constructing the exam structure and content. The SMEs coordinate with psychometricians who assist in the exam development and test validation processes. At OpenEDG Python Institute, we work closely with Python community experts and industry and education sector representatives to make sure our certification and exam standards address the actual needs of the market, and follow the principle "made by professionals, for professionals".

Exam Design and Development – the most important stage, in which the exam contents are created. It involves simultaneous cooperation of certification program managers, stakeholders, psychometricians, SMEs, test publishers, and developers who work together in order to create the framework for an exam, its structure, item format, delivery mode and format, scoring, as well as designing the actual exam items. The Exam Design and Development stage consists of six phases:
- Structure development: defining test specifications (the blueprint) such as number of sections, number of items, exam length, type of questions, scoring model, graphics or exhibits, presentation order, reporting groups, etc.
- Item Development: item writing, screening, technical reviews – defining the stems, correct answers and distractors; defining requirements for exhibits and graphics; technical proofs;
- Exhibit Development: constructing media, simulations, and graphics that supplement the exam items; exhibit implementation;
- Proofreading: language editing, second technical proof and scanning for typos; copyediting;
- Item selection and implementation: selecting the items that will be included in the item pool; creating source files and implementing them in the local Exam Testing System for internal review;
- Live Pool Deployment and first internal review – the exam is assembled and deployed in the testing environment. The first internal review of the exam is carried out in the simulated testing environment; the exam is launched and tested by the SMEs; instant corrections and amendments are made where necessary. The main purpose of this review is to locate and eliminate errors before releasing the exam for pilot testing (SMT).

Small Market Trial (SMT) – the Pilot Testing stage when the exam is administered among the beta testers and focus groups. Test candidates are also asked to mark exam items that may be misinterpreted, have poor wording, or have either no or more than the expected correct answers.

Final Review and Evaluation – an insight is made into the performance of individual exam items, and the exam in its entirety, which includes looking into such aspects as: diagnosing potential issues with item difficulty levels, diagnosing the correlation between exam items, identifying possible scoring and answer key issues, determining the assumed estimates of pass rates and time allocated for the exam. The final (amended/updated) exam version (the assembly of operational item pools and final specifications) is the resulting product of this stage, and is now ready for publishing.

Exam Publishing – the stage when the exam has been designed, tested, evaluated, and updated by the outcome of the Evaluation stage, and is now ready for release. The exam is labelled with a series code, and becomes available worldwide through OpenEDG Testing Service (TestNow™) as well as the global network of reputable testing centers. This stage requires close cooperation between the product manager and the exam publisher in order for the process to be effective, timely, and successful.

Exam Maintenance – exam design and development is a continuous process, so the Exam Maintenance stage takes place once the exam is live and test candidates begin to take it. At this stage, the exam's performance is monitored and analyzed to ensure that it meets the goals and assumptions set forth in the Market Research, Market Analysis, and Syllabus Development Stages. The data collected allows for the carrying out of post-publishing analyses and the updating of exams, which means the exam contents are revisited, and the whole exam design process starts over. During this process, the candidate experience and exam reputation are analyzed in order to make necessary changes to improve the testing experience and strengthen credibility and recognition of the certification program. Exam update frequency: once every two years after first publishing or after a specified number of test candidates has taken the exam; whichever happens first.

Evaluation Process

The OpenEDG Python Institute performs validation of its exams in alignment with the prescriptive guidance regarding educational and psychological assessment practices put forth in the Standards for Educational and Psychological Testing (AERA, APA, NCME), as well as the European Test User Standards and the European Test Review Model (EFPA, EAWOP).

The evaluation process consists of a thorough review of all available evidence gathered during the design, development, and implementation of the testing program, and involves an iterative collaboration between the test publisher, subject matter experts, and psychometricians. Further, data gathered from a field test of live respondents is comprehensively reviewed. Consequently, validation of the assessment and testing practices is carried out in a manner consistent with applicable industry best practices, ethical standards, and prominent research literature. This iterative process of collaboration between the publisher, subject matter experts, and psychometricians, as well as comparison of the evidence to applicable standards provides the basis for the findings and recommendations.

Item Response Theory (IRT): Verifying Unidimensionality

In comparison to traditional fixed-form exams, the Python Institute tests utilize a "random-random" sampling procedure to randomly sample one of a number of versions of each of the items from the item test bank. As such, no fixed-form versions of the exams exist, which assists in preventing cheating and piracy.

Item-level analyses are conducted under the guiding framework of Item Response Theory (IRT). In comparison to classical test theory (CTT), IRT is considered as the standard, if not preferred, method for conducting psychometric evaluations of new and established measures. At a high level, IRT is based on the premise that only two elements are responsible for a person's response on any given item: the person's ability (or abilities), and the characteristics of the item.

Development and validation of the Python Institute exams entail the use of a unidimensional IRT model based on the premise that correlations among responses to test questions can be explained by a single underlying trait (i.e. Python proficiency/ability). While traits/abilities like Python proficiency are complex and represent many different constituent skills and facts that are combined in specific ways, the claim of unidimensionality is that these components work together to manifest a coherent whole. Although the tests are structured around four to six topical sections, this is done to provide adequate domain sampling rather than to measure different traits.

While individuals may have strengths and weaknesses with respect to the topical sections on a unidimensional test, any systematic relationship among those topical sections should be explained by the effect of the single latent trait or ability (Python proficiency) upon the examinees' item responses. In alignment with the literature standard, unidimensionality is evaluated (and confirmed) through the use of a confirmatory factor analysis (CFA) model and review of goodness of fit statistics (RMSEA, CFI, TLI).

Item Response Theory (IRT): Model Overview

At a basic level, IRT models estimate mathematical equations in order to model the relationship between an examinee's probability of correctly responding to an item and their ability level. The basic unit of an IRT model is the Item Characteristic Curve (ICC), which estimates the probability of a given response based on a person's level of latent ability, wherein the shape and location of the curve is determined by the item characteristics estimated by the model parameters. While there are a variety of different forms an IRT model can take, IRT models of the form utilized for our test evaluations assume the probability of a given response is a function of the person's ability (theta θ), the difficulty of the item (b), and the discrimination of the item (a).

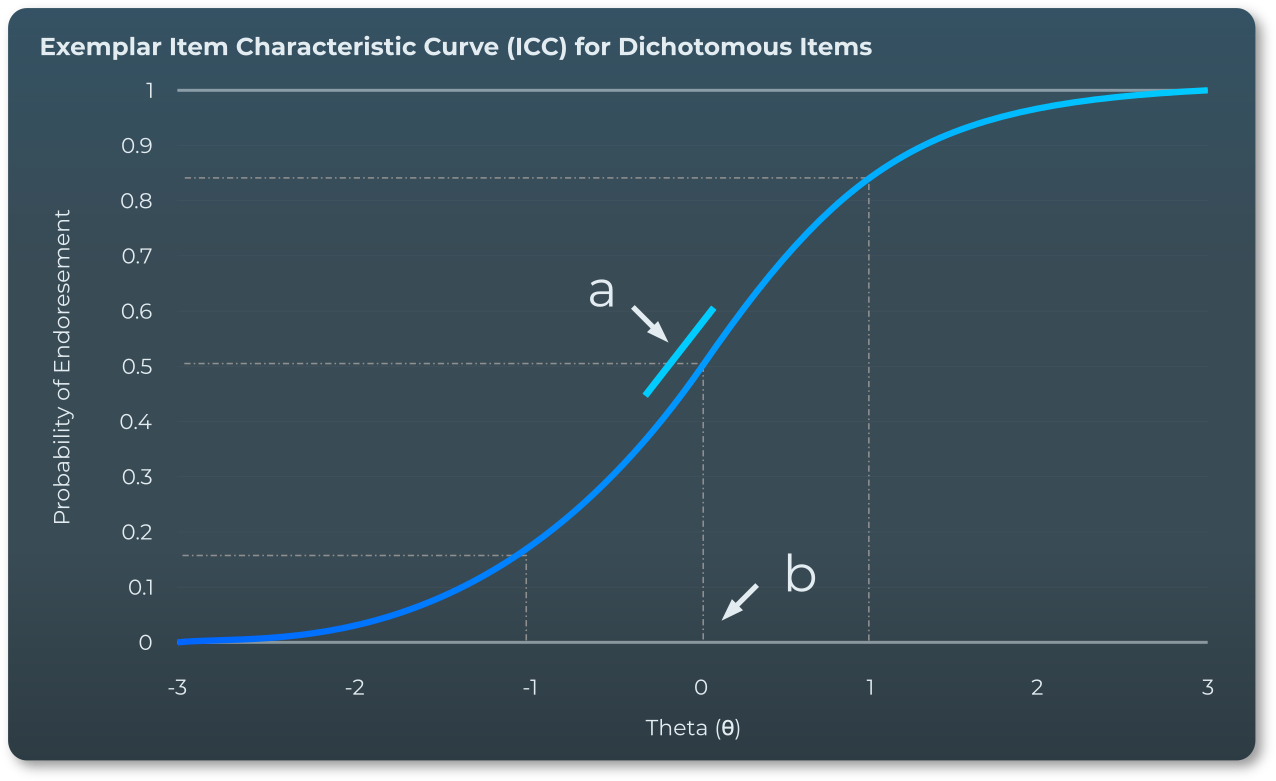
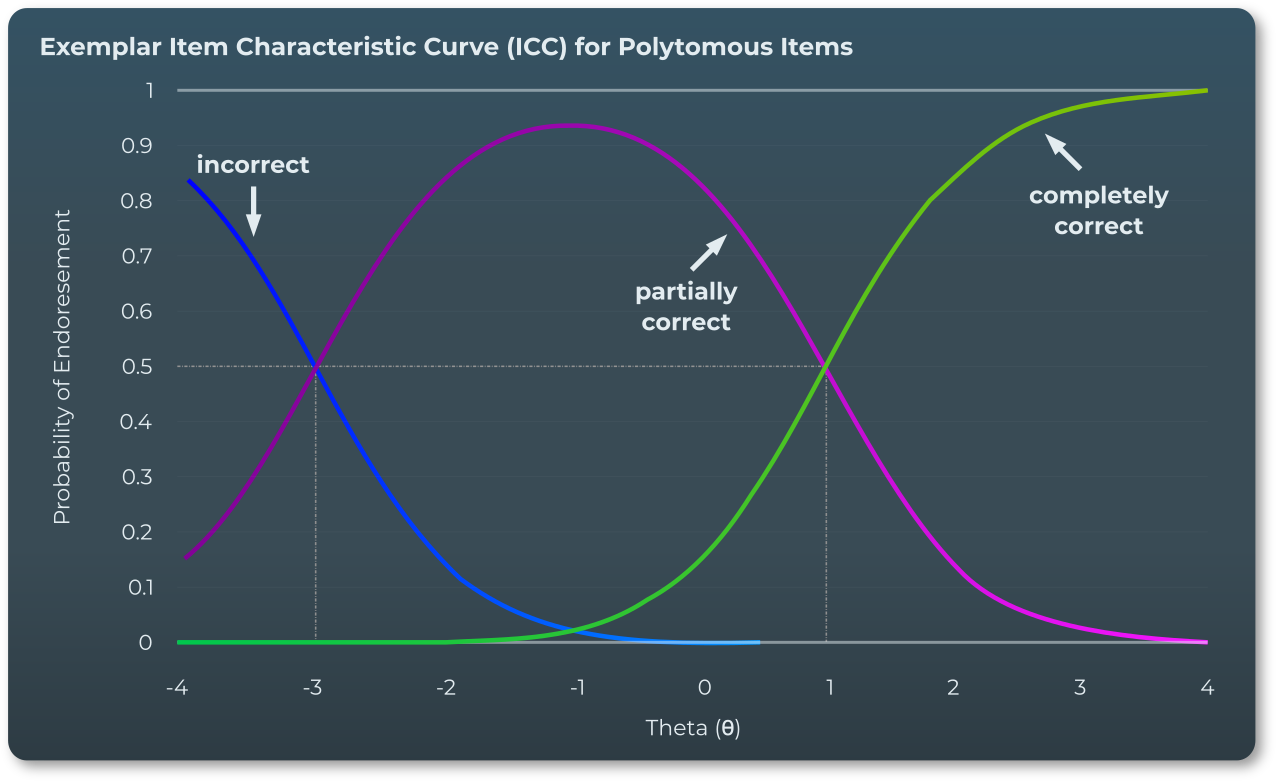
Generalized Partial Credit Model

Evaluation of the exams is conducted utilizing a specific form of IRT model referred to as the generalized partial credit model (GPCM), which allows for a mixture of dichotomous items (where a response is either completely right or wrong) and polytomous items (where examinees can receive partial credit for a partially-correct response). The GPCM model incorporates the following four parameters:

Difficulty parameter for partial credit threshold (b₁)
Difficulty parameter for full credit threshold (b₂)
Discrimination parameter (a) – describes how well the item differentiates ability
Person-level ability parameter (θ) – standardized measure of examinee ability level

Item Information Function (IIF)

The information provided by an item and a test can be evaluated in an IRT model by using the Item Information Function – IIF or I(θ). The information for an item is essentially an index of how precise or accurate the item is over the range of ability levels (θ). If an item is very precise and accurate for individuals of a given ability level, then the item is very informative regarding that ability level. The Item Information Function plot basically provides a visual representation of this, such that the highest point on the IIF curve corresponds to the ability level for which the item is most informative.

In addition, the peakedness of the IIF plots is also useful in that items with steep, narrow, peaked IIF curves denote that the item is highly informative over a specific range of ability. In contrast, shallow, less-peaked IIF curves denote items where a lesser amount of information is spread out over a wider range of ability levels.

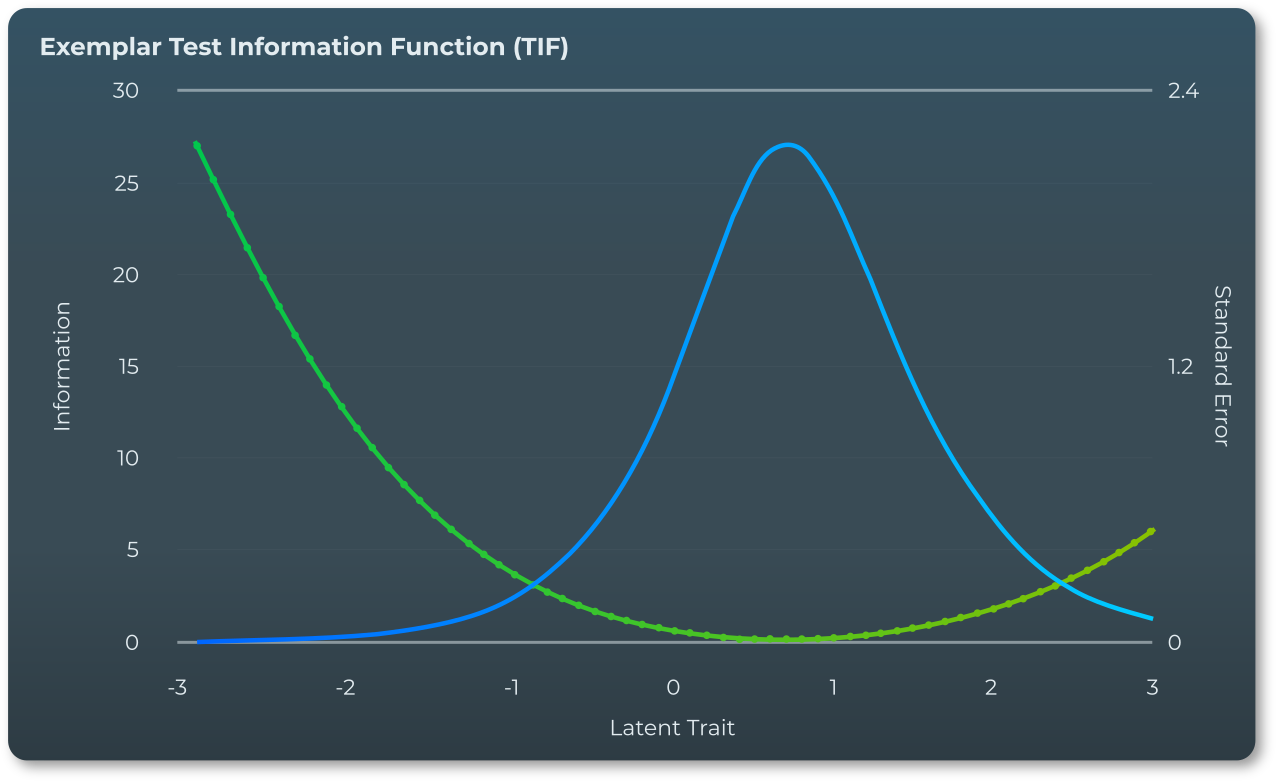
While the Item Information Function (IIF) represents the range of ability levels that each individual item is most informative over, the Test Information Function (TIF) represents the range of ability levels that the test as a whole is most informative over, and over which it functions most effectively. Just as the Item Information Function is related to how precise a given individual item is at different ability levels, the Test Information Function is related to how precise the test is across different ability levels.

This overall accuracy and precision is indexed through the inverse of the Standard Error of θ, which simply quantifies the expected error for any estimate along the range of ability levels (θ). In practical terms, when the TIF curve is concentrated over a belowaverage ability level (θ < 0), the test is most effective and provides estimates with lowest standard error for individuals with lower ability levels. When the TIF is concentrated (peaked) over higher ability levels (θ > 0), this indicates the test as a whole is most effective at evaluating above-average ability levels.

We make sure that the TIF plot is always reviewed to verify that our tests are effective in relation to the desired range of ability levels.